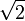Factoriza el polinomio

Factoriza el polinomio

p(x) =  X² +  (2√5) x + 2√5

Factorizar => buscar una raíz de p(x) => p(x)=0


 Usamos este ejemplo:

X² +  (2√5) x + 2√5 = 0

Utilizamos la fórmula para factorizar polinomios. Podemos ver cual es la parte a , b y c del polinomio.

Ahora otro polinomio:



p(x) = 6X² + 7x -3    =>     6X² + 7x -3 = 0

 lo igualamos a cero y vemos que es una ecuación de segundo grado así que usamos la fórmula para resolver las fórmulas de segundo grado:


 X=(+- B -√B²-4*A*C)/2*A = > => =>  X=(-7+-√49-4*6(-3))/2*6

  X=(-7+-√49-4*6(-3))/2*6   =  ( -7+-√121)/12     =    


  =   (-7+-11)/12  los dos resultados son: 1/3 y -3/2



x  -  1/3  es divisor de p(x)

buscamos divisiones con lo que vulgarmente llamamos regla de Ruffini:


 6X² + 7x -3 = (x - 1/3) * c(x)


                      6     7      -3

         1/3               2       3                      c(x)  6x + 9          
                 _______________
                 
                      6     9      0
                  


6X² + 7x -3  =  (x - 1/3) * (6x + 9)

Teorema del factor

El Teorema el factor

· x - a es un factor de P(x)  si solo si  a es raíz de P(x)

· x - a divide a p(x)

· p(x) es múltiplo de x - a

Demostración:

Teorema del resto

El Teorema del resto

Dice que :    P(x)  entre  x - a  da a un R que es un polinomio de 

                    grado cero y un c(x) siendo  R = P(a).

Demostración: 

                     P(x) = (x-a) * c(x) +R

                     P(a) = (a-a) * c(a) + R

      

                     P(a) = R

Ejercicio calcula el resto: 

       

Proposición (división entera)

En clase hemos dado la proposición de una división entera.
Primero vamos a ver que significa cada cosa :

D = dividendo     d = divisor     c = cociente     r = resto      

Ejemplo :   

X tiene que estar en :  Z(x)  Q(x)  y  R(x)


Si D y d pertenecen a los números enteros entonces c y r también.


Ahora :   D = d * c + r     con 0 más pequeño o igual que el resto y este más pequeño que el dividendo.

                  D(x) = d(x) * c(x) + r(x)

Ejemplo:  

Polinomios

Los polinomios son expresiones algebraicas (números, operaciones y letras) que tienen forma:

Está compuesto por:

Un monomio: es un polinomio con un término.

Término:expresión que está separada por los signos de suma o resta. ej: 20, 7x, -9X²

Para que sea un polinomio An debe ser distinta de cero.
























Y por último

i debe pertenecer a los números naturales.




Expresión analítica de un polinomio

Y= F (X)

Reconocer polinomios

Ejercicio de polinomios

Polinomio


Es una expresión matemática constituida por un conjunto finito de variables y coeficientes utilizando solamente operaciones de suma resta y multiplicación y utilizando exponentes enteros positivos


                  

                   ¿Es un polinomio?

En este ejercicio (que me ha traído más problemas de lo que me esperaba) se reflejan con un círculo los que son polinomios.

Al principio no lo entendí muy bien pero ahora que se que se pueden hacer operaciones de suma resta y multiplicación y no hacer raíces cuadradas como √X+5  o fracciones como 

X² + 3

——–    lo consigo entender mejor.

X - 1

DISPUTAS MATEMÁTICAS EN EL SIGLO XVI

Opinión sobre: http://historiaybiografias.com/disputas_matematicas/



A través de este artículo se puede ver el ansia que tenían estos matemáticos por descubrir las ecuaciones de tercer grado ya que desde el año 2500 a.C. se conocían las de segundo grado.



Del Ferro


Del Ferro encontró una fórmula que resolvía un tipo de ecuaciones de tercer grado, pero este señor no hizo públicos sus avances ya que prefirió dejárselos a amigos y familiares. Cuando murió sus escritos pasaron a manos de Fiore.


Tartaglia

Su verdadero nombre era Fontana pero fué apodado Tartaglia a causa de su tartamudez .
Tartaglia estaba estudiando ecuaciones de tercer grado y Fiore (quien tenía los resultados de Del Ferro) lo retó.
Fiore solo sabía hacer un tipo de ecuaciones así que tartaglia lo ganó haciendose así famoso.


Cardano

Cardano quien tuvo fama de persona poco querida se acercó a Tartaglia cono el fin de que este le enseñara a resolver ecuaciones de tercer grado, pero tardó bastante en conseguirlo y se lo enseño pero con la condición de que tenía que esperar a publicar un libro hasta que él lo hiciera. Cardano descubrió que el primero en resolverlas fue Del Ferro así que al no ser Tartaglia el primero publicó su libro primero.


Conclusión:

Hay que ver hasta donde escapaz de llegar la gente para hacerse famosa esta historia esta llena de engaños y más que por decubrir las ecuaciones de tercer grado yo las recordaré por sus engaños. 

Ecuación Diofántica y Térmas pitagóricas

Partimos de los cuadrados de una suma y la diferencia de cuadrados:

Hacemos la resta entre los cuadrados de una suma y la diferencia de cuadrados.

No contentos con eso seguimos divagando y hacemos lo mismo pero elevando m y n al cuadrado y nos da este resultado:

Tras haber hecho esto hemos hallado la ecuación Diofántica:

                                           X² + Y² = Z² 

Siendo:

· X = M² - N²

·Y = 2MN

·Z = M² + N²

Hacemos una proposición:

                      · X = M² - N²

Si:               ·Y= 2MN                                    Entonces:      X² + Y² = Z²

                       ·Z= M² + N²

Ahora hacemos Termas pitagóricas:

                   M              N               X              Y              Z

                    1                1               0               2              2

                    2                1                3               4              5

   

                    1                2               -3               4              5        

                    3                2                5              12            13

¿Es racional?

Hoy hemos comprobado si una suma de radicales es racional.

Para demostrar que es racional lo hemos hecho por reducción a lo absurdo:

Supongamos que es racional.
Lo igualamos a una letra y dejamos a un lado la raíz de 6 y como esta no es un número racional la igualdad tampoco lo es así que necesitamos un lema y este es:

 5+2*(raíz de 6) NO PERTENECE A LOS NÚMEROS RACIONALES

Ejercicios de radicales

En la clase de hoy hemos puesto a prueba lo que entendemos por ``número radical´´ con un sencillo ejercicio:






(no he conseguido escribirlo con lenguaje matemático, cuando descubra como se hace lo cambiaré)


·El primer ejercicio consistía en saber diferenciar lo que son números radicales, y son:

 La raíz de dos, la raíz cúbica de menos dos tercios, tres elevado a la un quinto y la raíz cúbica de menos dos.


·El segundo ejercicio consiste en averiguar si el resultado de esos dos radicales es un número radical:

Primero descomponemos el 12 y el 27, después sacamos el dos del primero y un tres del segundo, sumamos los números que hemos dejado fuera y ya lo tenemos.

Los números radicales

En las últimas clases de matemáticas nos hemos empezado a meter con los radicales y de aquí hubo una cosa que me llamó la atención, y es que hasta ahora no había tenido relacionado el siguiente concepto:  

= X

Xⁿ =a

Ejemplo: 

                                 · X=

                                 · χ²=2

                                                                   

Las primeras clases

En las primeras clases de matemáticas hemos aprendido a leer el lenguaje matemático.

De aquí el aspecto que más me ha llamado la atención han sido las proposiciones o teoremas.  Los tipos de proposiciones son:

·Proposición directa: Es la que nos han enunciado.                       Ejemplo: P=>Q

·Proposición contraria: Negamos la enunciada.

                    Ejemplo: No P=> No Q

·Proposición recíproca: Es la inversa de la directa.

                    Ejemplo: Q=>P

·Proposición contrarecíproca: Negamos la recíproca.

                    Ejemplo: No Q=> No P

Inicio

Este blog ha sido creado para el estudio y comprensión de las matemáticas. Aquí relataré todo aquello que estudie y que me parezca relevante. Estará activo todo este año y el siguiente.